Site Changes
Still a bit occupied with other projects. One of the big time activities is the migration of my main website from the MobileMe site hosted by Apple to its new home:
CrankAstronomy.org
Update your bookmarks accordingly as the old site will go offline sometime this summer.
Note that I'm also changing the name to bring it more in line with the kind of projects I'm developing today compared to when I started. Right now it is a simple duplication of the site at my old location. The new site layout will change with time as the hosting service has a number of capabilities not available at my previous provider and it will take time for me to install the new features.
Mythbusters: Behind the Myths Tour
In addition, I recently attended a performance of the
Mythbusters: Behind the Myths Tour
Unfortunately, the tour has only a few more stops, but I highly recommend it if it comes to your area.
Adam Savage (whom I've seen at places like DragonCon) and Jamie Hyneman do an excellent stage show, performing some of the smaller demonstrations that can be done on a stage. Their show includes audience participation (probablyhalf their projects required one or more volunteers from the audience) and Adam and Jamie take turns fielding questions from the audience. The show is about two hours long with one 15 minute intermission.
They were also promoting their new site: www.tested.com
The Reason Rally was also going on in my area that day, so there were a few science and skepticism luminaries in the audience, including James Randi (wikipedia), Lawrence Krauss (A Universe from Nothing), and Richard Dawkins (wikipedia).
Sunday, March 25, 2012
Sunday, March 18, 2012
An Exploration of the Lagrange Points
I was hoping to have a different post ready for this week, but recent solar activity kept me directed on other projects this week.
However, while browsing around some of my favorite sites, I discovered an entry in Wired's dot Physics column that was very relevant to topics I've discussed recently on this blog:
James Webb Space Telescope and L2 Orbits
Dr. Allain goes into a fair amount of detail on analyzing the gravitational and non-gravitational forces that will act on JWST at the L2 Lagrange point, even including the question of stability of bodies at this location. A similar analysis could be done for L1 and L3. We already have a small fleet of spacecraft at the Sun-Earth L1 point (YouTube), and WMAP operated at L2, but don't yet have a good use for the Sun-Earth L3 point (maybe a full-time solar observatory for maintaining 360 degree coverage of solar activity?).
Perhaps the Geocentrists might find this analysis useful in meeting the Lagrange Point challenge?
I'll use this opportunity to show off a few tests of my explorations of the Lagrange points using my n-body code (see Doin' Real Science: Simulating Particles). I've run some simulations of the Sun (red) & Jupiter (green) and placed test particles (cyan x) of negligible mass (spacecraft?) near the unstable Lagrange points (L1, L2, L3) and similar test particles (magenta +) near the stable Lagrange points at L4 & L5.
In the movie above, I've set the origin of the coordinate system at the center of the Sun and turned off the particle trails. As the movie plays, we see the particles near the stable Lagrange Points (magenta) pretty much stay on the orbit of Jupiter, while the particles at the unstable points (cyan) move substantially. But we can get a much better idea of what's happening if we transform to a coordinate system that rotates around the Sun with Jupiter.
Above we see the motions in a frame that rotates around the Sun with Jupiter. We get a better idea of how the unstable points either migrate away from the planet moving into a more solar orbit, or go into orbit around Jupiter. We see that the particles at the stable points (magenta) actually move very little. Of the two sets of five particles ahead and behind the orbit of Jupiter, the central particle is at maximum point of stability and we see they hardly move at all.
If I zoom in close to Jupiter, in the simulation above, we see the two satellites nearest on either side of Jupiter move into complex orbits around the planet. The two satellites furthest from Jupiter on either side of the planet move outward into solar orbits. But we also have two remaining points on either side of the planet, which correspond to the satellites I placed precisely at L1 & L2. For a simulation of one orbit of Jupiter (12 years), they've done a great job of staying in place since these two points are unstable, but I suspect they would start migrating away if I ran the simulation for longer.
Enjoy!
However, while browsing around some of my favorite sites, I discovered an entry in Wired's dot Physics column that was very relevant to topics I've discussed recently on this blog:
James Webb Space Telescope and L2 Orbits
Dr. Allain goes into a fair amount of detail on analyzing the gravitational and non-gravitational forces that will act on JWST at the L2 Lagrange point, even including the question of stability of bodies at this location. A similar analysis could be done for L1 and L3. We already have a small fleet of spacecraft at the Sun-Earth L1 point (YouTube), and WMAP operated at L2, but don't yet have a good use for the Sun-Earth L3 point (maybe a full-time solar observatory for maintaining 360 degree coverage of solar activity?).
Perhaps the Geocentrists might find this analysis useful in meeting the Lagrange Point challenge?
I'll use this opportunity to show off a few tests of my explorations of the Lagrange points using my n-body code (see Doin' Real Science: Simulating Particles). I've run some simulations of the Sun (red) & Jupiter (green) and placed test particles (cyan x) of negligible mass (spacecraft?) near the unstable Lagrange points (L1, L2, L3) and similar test particles (magenta +) near the stable Lagrange points at L4 & L5.
 |
| Click for larger image or download movie here (11MB) |
In the movie above, I've set the origin of the coordinate system at the center of the Sun and turned off the particle trails. As the movie plays, we see the particles near the stable Lagrange Points (magenta) pretty much stay on the orbit of Jupiter, while the particles at the unstable points (cyan) move substantially. But we can get a much better idea of what's happening if we transform to a coordinate system that rotates around the Sun with Jupiter.
 |
| Click for larger image or download movie here (11MB) |
 |
| Click for larger image or download movie here (11MB) |
Enjoy!
Sunday, March 11, 2012
Geocentrism & Cosmological Redshift
Laurence Krauss had a simple demonstration (see Reading: A Universe from Nothing by Lawrence Krauss) of how expansions where the recessional velocity is proportional to the distance of the object create a system where a center cannot be defined from inside the distribution. This is the same type of expansion revealed in extra-galactic redshifts.
This type of expansion is more generally called homologous expansion. Ned Wright as some graphics describing various types of expansions on his cosmology site: "Distortion during Expansion of the Universe"
Stepping Through the Expansion
Paralleling the treatment in Krauss, we'll first take a few snapshots of the positions of our galaxies at three different times. The positions of the galaxies, where our observers are located, are called the co-moving frame, and are carried with the expansion. At the first time, all the points (galaxies) are located at the vertices of unit squares, so we have galaxies at (x,y)= (0,0), (1,0), (1,1), etc. which are represented by the red dots in this graphic. At each time step we expand the distance between each of the points.
At the next timestep, the distances between each of the points is expanded by a factor of 1.2. The co-moving coordinates of each galaxy remain the same, but the measured distances between the galaxies has increased.
For good measure, we'll expand the scale once more by a factor of 1.4 over the original scale. Assuming the same time between each step, this corresponds to a constant rate of expansion.
To explore this exercise yourself, print out the three graphs above on thin paper (sufficiently translucent that you can read other material trough it, or are able to hold it up to a light).
Now we overlay the three plots, lining up the dots at (0,0), representing our home galaxy, for each plot. If you've printed these out on sufficiently translucent paper, you should be able to line up the three pages (or at least two of the pages) and see through them to see the overall picture. When properly aligned, it would look something like Figure 4:
Here we see an analog of the cosmological motions with how the dots overlap, corresponding to later times. The galaxy at (0,0) stays fixed, the (apparent) center of the motion. But as we look at objects away from the center, the dots marking the galaxies nearest the center are still so close, the dots corresponding to different times slightly overlap - their velocities are low. But further out, the distances between the corresponding galaxies (red-to-green-to-blue) get further apart for the same amount of time. Therefore the galaxies further away from the center appear to be moving faster. The greater separation will be in proportion to the distance of the object from the center, analogous to the Hubble law.
But suppose we want to see how things look from one of the other galaxies?
Let's adjust the plot so we observe the expansion from the galaxy at appears to start at the position (2,1) in the first graphic. We can do the same with our printed pages. Be careful to align the SAME co-moving galaxy of the observer on each page. So we overlay the corresponding point in the remaining plots and get
Here we see the exact same thing as before. The galaxy at (2,1) corresponding to our observer remains motionless in this frame, while as we move further out, we see the galaxies appear to be organized concentrically around this new 'center', with low velocities near the observer galaxies and higher velocities further away.
This analogy also works in 3-dimensions.
This is why we can say the Hubble expansion cannot define a center. To any observer, located anywhere, they will perceive themselves the center of the expansion.
We're still in the Center of the Circle!
One of the popular responses to the fact demonstrated above is how we appear to be in the center of galaxy catalogs such as the SDSS survey. Note that I could have expanded the assumption of uniformity above by expanding the plot of points (galaxies) such that the edge was not visible - and the conclusions would not be altered.
Delusions of Geocentric Quantization...
However, as I demonstrated in some posts in my quantized redshifts series, a uniform distribution in space, which is magnitude limited (i.e. there are galaxies fainter than can be detected by our instruments) will exhibit a similar distribution with the galaxies which we can detect. For details, see:
That this works provides a consistency check against our other assumptions, such as the redshifts being an actual measure of distance and not intrinsic properties of the galaxies.
This type of expansion is more generally called homologous expansion. Ned Wright as some graphics describing various types of expansions on his cosmology site: "Distortion during Expansion of the Universe"
Stepping Through the Expansion
Paralleling the treatment in Krauss, we'll first take a few snapshots of the positions of our galaxies at three different times. The positions of the galaxies, where our observers are located, are called the co-moving frame, and are carried with the expansion. At the first time, all the points (galaxies) are located at the vertices of unit squares, so we have galaxies at (x,y)= (0,0), (1,0), (1,1), etc. which are represented by the red dots in this graphic. At each time step we expand the distance between each of the points.
 |
| Figure 1: scale = 1.0 |
At the next timestep, the distances between each of the points is expanded by a factor of 1.2. The co-moving coordinates of each galaxy remain the same, but the measured distances between the galaxies has increased.
 |
| Figure 2: scale = 1.2 |
For good measure, we'll expand the scale once more by a factor of 1.4 over the original scale. Assuming the same time between each step, this corresponds to a constant rate of expansion.
 |
| Figure 3: scale = 1.4 |
To explore this exercise yourself, print out the three graphs above on thin paper (sufficiently translucent that you can read other material trough it, or are able to hold it up to a light).
Now we overlay the three plots, lining up the dots at (0,0), representing our home galaxy, for each plot. If you've printed these out on sufficiently translucent paper, you should be able to line up the three pages (or at least two of the pages) and see through them to see the overall picture. When properly aligned, it would look something like Figure 4:
 |
| Figure 4: Overlay at (0,0) |
Here we see an analog of the cosmological motions with how the dots overlap, corresponding to later times. The galaxy at (0,0) stays fixed, the (apparent) center of the motion. But as we look at objects away from the center, the dots marking the galaxies nearest the center are still so close, the dots corresponding to different times slightly overlap - their velocities are low. But further out, the distances between the corresponding galaxies (red-to-green-to-blue) get further apart for the same amount of time. Therefore the galaxies further away from the center appear to be moving faster. The greater separation will be in proportion to the distance of the object from the center, analogous to the Hubble law.
But suppose we want to see how things look from one of the other galaxies?
Let's adjust the plot so we observe the expansion from the galaxy at appears to start at the position (2,1) in the first graphic. We can do the same with our printed pages. Be careful to align the SAME co-moving galaxy of the observer on each page. So we overlay the corresponding point in the remaining plots and get
 |
| Figure 5: Overlay at (2,1) |
Here we see the exact same thing as before. The galaxy at (2,1) corresponding to our observer remains motionless in this frame, while as we move further out, we see the galaxies appear to be organized concentrically around this new 'center', with low velocities near the observer galaxies and higher velocities further away.
This analogy also works in 3-dimensions.
This is why we can say the Hubble expansion cannot define a center. To any observer, located anywhere, they will perceive themselves the center of the expansion.
We're still in the Center of the Circle!
One of the popular responses to the fact demonstrated above is how we appear to be in the center of galaxy catalogs such as the SDSS survey. Note that I could have expanded the assumption of uniformity above by expanding the plot of points (galaxies) such that the edge was not visible - and the conclusions would not be altered.
Delusions of Geocentric Quantization...
However, as I demonstrated in some posts in my quantized redshifts series, a uniform distribution in space, which is magnitude limited (i.e. there are galaxies fainter than can be detected by our instruments) will exhibit a similar distribution with the galaxies which we can detect. For details, see:
- Quantized Redshifts. IX. Testing the Null Hypothesis
- Quantized Redshifts. X. Testing Our "Designer Universe"
- Quantized Redshifts XI. My Designer Universe Meets Some Data and What's Next...
That this works provides a consistency check against our other assumptions, such as the redshifts being an actual measure of distance and not intrinsic properties of the galaxies.
Sunday, March 4, 2012
The Geocentrists' 3-Body "Problem"
Here I'll examine a 3-Body case of two large planets (which I'll call "Earth" & "Jupiter") orbiting a star ("Sun").
Technically, Kepler's laws no longer apply in their absolute form, because we have more than two bodies. However, science always works with approximations, in part because there is no absolute perfect system of measurement. We cannot measure to arbitrary high precision. In these cases, what becomes important is does the technique work good enough to use for a given problem. We don't know the exact locations of the electrons in the computer you're using to read this, but we know their position, and what they are doing, good enough to make the device work with reasonable reliability.
In this 3-body case, the important question is not "do Kepler's laws apply", but by how much does the system deviate from Kepler's laws?
For this run of my N-body code (see Doin' Real Science: Simulating Particles), I'll choose a time step of 0.0001 years.
Time step = 0.0001 years = 0.036525 days ~ 52m 35s.
So my timestep size updates the simulation approximately each hour, and if I run the simulation for 200,000 steps, we have the equivalent of 20 years of total simulation time.
I'll also add an additional velocity of 0.01 AU/year in the y-direction to make the center-of-mass motion more evident.
Since in the real case, the deviations we're looking for are very small, we'll make our additional objects in the system much larger so the deviations will be more readily visible. We'll choose the mass of the Sun for the primary body, but we'll assign our "Earth" as 100 Earth masses (about 0.0003 solar masses), and our "Jupiter" as 10000 Earth masses (about 0.003 solar masses). Here's the table of my input parameters:
Model: 3-Body Problem (A)
Particle Count= 3
Interaction=
Q Object Mass ------------------ position -------------------
-------------------- velocity ---------------------
1) 0 Sun 1.00000e+00 Msun x=( 0.000000e+00, 0.000000e+00, 0.000000e+00) AU
v=( 0.000000e+00, 1.000000e-02, 0.000000e+00) AU/yr
2) 0 Earth 3.00349e-04 Msun x=( 1.000003e+00, 0.000000e+00, 0.000000e+00) AU
v=( 0.000000e+00, 6.293177e+00, 0.000000e+00) AU/yr
3) 0 Jupiter 3.00349e-03 Msun x=( 5.202887e+00, 0.000000e+00, 0.000000e+00) AU
v=( 0.000000e+00, 2.764594e+00, 0.000000e+00) AU/yr
The '0' in the column labelled 'Q' means I've made the Sun and planets without a significant electric charge.
My python version runs this simulation in a few minutes on a 2.8GHz Intel. Here's a plot of the resulting paths in the coordinate system of the input position and velocity values.
The blue path is the orbit of "Jupiter" and the green path is the orbit of "Earth". In the center, barely visible on this scale, is the red path representing the motion of the Sun. We zoom in on this to better plot the motion:
Here we see the red curve of the Sun's motion. The dashed line is the motion of the center-of-mass of the system in the originally defined coordinate system. The large wave motion of the red line is due to the balance with the motion of "Jupiter" around the center-of-mass. However, you can see a smaller wiggle motion along the Sun curve. This is due to the additional perturbation created by the motion of the "Earth" around the center-of-mass.
It's difficult to get a clear understanding in the input coordinate system, so let's convert all of our positions into the center-of-mass (CM) frame for the entire system, using the technique outlined in the earlier post (see Geocentrism & the Barycenter. II.):
This looks a lot more interesting. In the CM frame, the orbits now look much more like circles to the limit of the plotting precision. The units in the x- and y-directions are AUs.
Let's take a closer look at the Earth's orbit (green):
The orbit looks rather thick. This is due to the Sun's motion around the CM and the Earth's orbit adjusting. Remember that the Sun's motion around the CM is dominated by the motion of "Jupiter". In the CM frame, the trajectory of the "Earth" wobbles around the Sun. The forces to make this happen just work.
We can zoom in to the red curve in the center to see the motion of the Sun around the center-of-mass.
The main circular motion of the CM is due to the massive planet, "Jupiter", but smaller wiggles are due to the Earth's motion. The reaction force of the "Earth" on the Sun moves the Sun by a tiny amount, which is mathematically constrained to balance around the center of mass. It is the superposition of these motions around the center-of-mass that allows us to detect multiple extrasolar planets by the radial velocity method (wikipedia).
Now we zoom back out to full scale again, and switch to a coordinate system so the Sun is fixed at the origin (0,0,0) of the coordinate system.
At this scale, to the eye, the orbits of the "Earth" and "Jupiter" appear very circular. I had chosen input positions and velocities consistent with circular orbits using Kepler's laws. So far, a Keplerian approximation used for originally defining the orbits looks like it's holding up pretty good, at least to the pixel resolution of this plot.
We can take a closer look a the Earth's orbit in this Sun-centered coordinate system.
Now the Sun is the red dot fixed at the center of the plot. The orbit of "Earth" still looks pretty close to a circular orbit, extending to 1AU along along the coordinate axes, to the pixel resolution. The shape in the center is the wiggling trajectory of the center-of-mass motion around the Sun in this frame. Here we take a closer look:
This motion mirrors the motion of the Sun around the around the center-of-mass (note previous figure). By the way, on this scale, the radius of the Sun is about 695,500km/149,598,000km = 0.00465 AU so the center-of-mass lies far outside the surface of the Sun.
If we want to see some differences, we need to zoom in even more on the green curve of the Earth's orbit.
At this scale, we see that the orbit path looks much thicker, like there might be overlapping paths. So we zoom in some more:
At this scale, each mark in the grid is 0.002AU = 2*149000 km = 299,000 km, less than the distance of the Earth from the Moon. The difference in position for each orbit of the Earth is about 1/10 of this, or about 30,000 km. Because I increased the planet masses, this deviation is actually far larger than it would be in the real case.
For this scale, this is actually pretty good accuracy for the technique utilized. At full scale, we cannot easily distinguish the deviation of the orbit from a circle. We must be very close to see it. Part of the motion is due to the perturbations created by the presence of "Jupiter", but part is also due to the fact that each step in the calculation, the next position is computed only to a finite level of precision and some accuracy is lost. Yet in spite of these errors, orbit is almost indistinguishable from the original defined orbit.
The notion that a theory or model must provide perfect precision is a delusion propagated by pseudo-scientists. Models are always limited by our measuring precision, on both the input and output parameters.
Imagine driving down the road, at 65 mph, and seeing a sign for you destination, 130 miles away. With this information, I estimate 2 hours to my destination. Is that perfectly accurate? No. It does not include small changes in speed due to uphill or downhill travel, or even that tap on the brakes as you see the state trooper around the bend and realize you're travelling a bit over the speed limit. Is my estimate of 2 hours inaccurate? Yes.
But is my estimate of 2 hours useless? Not really. It is still perfectly acceptable for planning my travel, and like most data, can be revised as I get closer to my destination (and incorporate bathroom or gas stops, etc.)
The inaccuracy of the estimate does not invalidate the equation (time) = (distance travelled)/(speed). This in itself is an approximation based on the assumption of constant speed. But even if you are not travelling at constant speed, it does not become grossly wrong.
So it is with Kepler's Laws. When applied to the other planets in the solar system, it is not perfectly exact - but it is not grossly wrong either. The other bodies in the solar system must be much more massive to perturb the other planets sufficiently that Kepler's Laws become totally useless, contrary to Mr. Martin's pedantic claims.
Technically, Kepler's laws no longer apply in their absolute form, because we have more than two bodies. However, science always works with approximations, in part because there is no absolute perfect system of measurement. We cannot measure to arbitrary high precision. In these cases, what becomes important is does the technique work good enough to use for a given problem. We don't know the exact locations of the electrons in the computer you're using to read this, but we know their position, and what they are doing, good enough to make the device work with reasonable reliability.
In this 3-body case, the important question is not "do Kepler's laws apply", but by how much does the system deviate from Kepler's laws?
For this run of my N-body code (see Doin' Real Science: Simulating Particles), I'll choose a time step of 0.0001 years.
Time step = 0.0001 years = 0.036525 days ~ 52m 35s.
So my timestep size updates the simulation approximately each hour, and if I run the simulation for 200,000 steps, we have the equivalent of 20 years of total simulation time.
I'll also add an additional velocity of 0.01 AU/year in the y-direction to make the center-of-mass motion more evident.
Since in the real case, the deviations we're looking for are very small, we'll make our additional objects in the system much larger so the deviations will be more readily visible. We'll choose the mass of the Sun for the primary body, but we'll assign our "Earth" as 100 Earth masses (about 0.0003 solar masses), and our "Jupiter" as 10000 Earth masses (about 0.003 solar masses). Here's the table of my input parameters:
Model: 3-Body Problem (A)
Particle Count= 3
Interaction=
Q Object Mass ------------------ position -------------------
-------------------- velocity ---------------------
1) 0 Sun 1.00000e+00 Msun x=( 0.000000e+00, 0.000000e+00, 0.000000e+00) AU
v=( 0.000000e+00, 1.000000e-02, 0.000000e+00) AU/yr
2) 0 Earth 3.00349e-04 Msun x=( 1.000003e+00, 0.000000e+00, 0.000000e+00) AU
v=( 0.000000e+00, 6.293177e+00, 0.000000e+00) AU/yr
3) 0 Jupiter 3.00349e-03 Msun x=( 5.202887e+00, 0.000000e+00, 0.000000e+00) AU
v=( 0.000000e+00, 2.764594e+00, 0.000000e+00) AU/yr
The '0' in the column labelled 'Q' means I've made the Sun and planets without a significant electric charge.
My python version runs this simulation in a few minutes on a 2.8GHz Intel. Here's a plot of the resulting paths in the coordinate system of the input position and velocity values.
 |
| (Click to enlarge) |
 |
| (Click to enlarge) |
It's difficult to get a clear understanding in the input coordinate system, so let's convert all of our positions into the center-of-mass (CM) frame for the entire system, using the technique outlined in the earlier post (see Geocentrism & the Barycenter. II.):
 |
| (Click to enlarge) |
Let's take a closer look at the Earth's orbit (green):
 |
| (Click to enlarge) |
We can zoom in to the red curve in the center to see the motion of the Sun around the center-of-mass.
 |
| (Click to enlarge) |
The main circular motion of the CM is due to the massive planet, "Jupiter", but smaller wiggles are due to the Earth's motion. The reaction force of the "Earth" on the Sun moves the Sun by a tiny amount, which is mathematically constrained to balance around the center of mass. It is the superposition of these motions around the center-of-mass that allows us to detect multiple extrasolar planets by the radial velocity method (wikipedia).
Now we zoom back out to full scale again, and switch to a coordinate system so the Sun is fixed at the origin (0,0,0) of the coordinate system.
 |
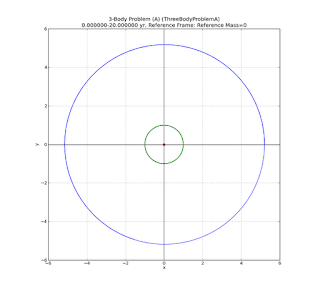| (Click to enlarge) |
At this scale, to the eye, the orbits of the "Earth" and "Jupiter" appear very circular. I had chosen input positions and velocities consistent with circular orbits using Kepler's laws. So far, a Keplerian approximation used for originally defining the orbits looks like it's holding up pretty good, at least to the pixel resolution of this plot.
We can take a closer look a the Earth's orbit in this Sun-centered coordinate system.
 |
| (Click to enlarge) |
 |
| (Click to enlarge) |
If we want to see some differences, we need to zoom in even more on the green curve of the Earth's orbit.
 |
| (Click to enlarge) |
 |
| (Click to enlarge) |
For this scale, this is actually pretty good accuracy for the technique utilized. At full scale, we cannot easily distinguish the deviation of the orbit from a circle. We must be very close to see it. Part of the motion is due to the perturbations created by the presence of "Jupiter", but part is also due to the fact that each step in the calculation, the next position is computed only to a finite level of precision and some accuracy is lost. Yet in spite of these errors, orbit is almost indistinguishable from the original defined orbit.
The notion that a theory or model must provide perfect precision is a delusion propagated by pseudo-scientists. Models are always limited by our measuring precision, on both the input and output parameters.
Imagine driving down the road, at 65 mph, and seeing a sign for you destination, 130 miles away. With this information, I estimate 2 hours to my destination. Is that perfectly accurate? No. It does not include small changes in speed due to uphill or downhill travel, or even that tap on the brakes as you see the state trooper around the bend and realize you're travelling a bit over the speed limit. Is my estimate of 2 hours inaccurate? Yes.
But is my estimate of 2 hours useless? Not really. It is still perfectly acceptable for planning my travel, and like most data, can be revised as I get closer to my destination (and incorporate bathroom or gas stops, etc.)
The inaccuracy of the estimate does not invalidate the equation (time) = (distance travelled)/(speed). This in itself is an approximation based on the assumption of constant speed. But even if you are not travelling at constant speed, it does not become grossly wrong.
So it is with Kepler's Laws. When applied to the other planets in the solar system, it is not perfectly exact - but it is not grossly wrong either. The other bodies in the solar system must be much more massive to perturb the other planets sufficiently that Kepler's Laws become totally useless, contrary to Mr. Martin's pedantic claims.
"Pedantry and mastery are opposite attitudes toward rules. To apply a rule to the letter, rigidly, unquestioningly, in cases where it fits and in cases where it does not fit, is pedantry ... To apply a rule with natural ease, with judgment, noticing the cases where it fits, and without ever letting the words of the rule obscure the purpose of the action or the opportunities of the situation, is mastery." -George Polya, mathematician (1887-1985)
Subscribe to:
Posts (Atom)