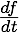d/dt: The Root of Evolution

There is an ambiguity in the use of the term “Evolution” in the whole Creation vs. Evolution “controversy”. 

Among scientists, the term “Evolution” by itself is usually assumed to mean biological evolution.  There are a number of other scientific uses of the term that are usually referenced with a qualifier.  In astronomy, there are subfields such as stellar evolution and cosmic chemical evolution and similar uses of the term 'evolution'.  All of these terms refer to how the structure, chemical abundances, and other characteristics of astronomical objects changes with time.

When wielded by a creationist, the term 'evolution' can mean any or all of the above.  In arguments, they will often lump Big Bang cosmology in with their claims about biological evolution. 

But in this case and others, it reveals yet another fundamental misunderstanding among creationists:

Evolution is built into the very fundamental physical laws that govern the Universe.

Evolution in time is a part of every major physical theory.  These theories incorporate the behavior of some measurable property as time progresses.  This characteristic is incorporated into the mathematical form of the theory through a term called a time derivative (Wikipedia).  There are two popular forms used to designate time derivatives.  There is the total derivative (Wikipedia) of, for example the quantity, f, with respect to time,

and the partial derivative (Wikipedia), with the more unusual symbols

(The details how these two forms are used in physics and mathematics are not really relevant to this discussion.)

The derivative most people would be familiar with is the speedometer on their car.  Speed is the time derivative of distance traveled (so the speedometer displays the time derivative of the odometer).  Conversely, the odometer in the integral of the speedometer, adding up the different speeds at different times to compute the total distance traveled.

Here's some of the fundamental theories where change with respect to time is an important part of the theory.

 - Newton's theory of motion and gravitation

where the force, F, is defined as the change in momentum with time, and this is equated to the gravitational force.  Note that in the case of gravity, the force is directed along the line between the two masses, designated M and m.  The full 3-dimensional form of this theory is used for predicting where planets and asteroids move with time, as well as the engineering application of moving human-made satellites around in space.

 - Maxwell's electromagnetism
               

Here, the equations are much more complex than Newton's theory of gravity.  This complexity is related to the coupled nature of electricity and magnetism.  The quantities in bold represent 3-dimension vector fields, in this case, the electric field, E, and the magnetic field, B.  The inverted triangle symbol, called nabla, is called an operator, which does specific manipulations on vector quantities.  In general, E and B can vary in space as well as time.  In this equation, the time derivative is a partial time derivative.  These equations are applied in the design of electrical circuits, especially circuits which use custom-designed components, as well as antenna design and the study of plasmas.

 - Schrodingers equation

This equation solved the mysteries of atomic structure and chemistry.  While the equation might look trivial, the quantity H is not a variable but an operator, similar to the vector operators above, which is a mathematical form the contains information about how energy (kinetic and potential) are stored in the system.  This equation not only solved the mystery of atomic spectra (Wikipedia) but also the structure of matter and provided the foundations of semiconductor electronics.  Today this equation is solved on computers for complex molecules to determine their properties before they are synthesized in the lab, the field of Computational Chemistry (Wikipedia).

I could describe more, but these three fundamental equations actually form the basis of much of the technology we've have developed in the twentieth century and how the system changes with time is part of every one of them!

Solving any of these equations for a general system, with time dependence, is a very difficult task.  It is only in the past fifty years or so, with the advent of modern computers, that progress has been made in realistic systems.  Prior to modern computers, the analysis was often restricted to systems with simple behavior in time, or even static, steady-state systems, where the time derivative is actually zero.  In this case, solutions could often be found through combination of known mathematical functions.  Mathematical techniques did not exist to solve them in the more general applications, or they had to be solved numerically by hand and were so tedious and complex it might take a researcher years just to solve a small system, assuming they didn't make a mistake.

Much of engineering is based on steady-state, or static solutions.  Many of the textbook formulas that  engineering students are often taught to accept as 'gospel' are often derived by physics students from more fundamental physics principles.  You want a bridge to be a stable structure for a long period of time so you look for solutions to the equations where the time-derivative of the velocity is zero - where all the forces exactly balance - indicating that it is a fixed solution for the system.   Most people prefer these characteristics in the products they purchase, from their homes to their cars.  They want any change in the system with time to be slow, to make the life expectancy of their purchase long.

But around 1900, researchers were beginning to realize that the simple, steady-state systems that they were studying mathematically were just the tip of the iceberg when it came to what was possible with these so-called 'simple' mathematical principles behind physics.  Even relatively simple physical principles, expressed as differential equations (Wikipedia) could yield surprising complex solutions that were not regular, and had many characteristics that, at first glance, might be regarded as random. 

This new complexity arises as we try to analyze more complex systems and the physical laws must be 'coupled' in different ways,  making the resulting equations a nonlinear system (Wikipedia).  For example, the Lorenz attractor arises in the study of convection, where where the density of a gas at different temperatures becomes a driving force under the action of gravity  (Wikipedia).

Consider the case of stellar evolution.  Astrophysicists first studied simple stars in a steady-state configuration.  They were able to do this using just the theory of gravity and the gas laws, before it was known that stars were powered by nuclear reactions.  Later, they realized that the nuclear reactions in the core of the star would change the composition of the core and this composition change would change the behavior of this hot plasma which would change the structure of the star.  In turn, the change in structure would create changes in the nuclear reactions and this feedback mechanism would create a situation where the star's structure and composition would change over time.  That is stellar evolution in a nutshell, a picture that did not reach observational, experimental, and theoretical maturity until the latter half of the 20th century.

As we analyze more complex systems, it becomes clear that these couplings between different physical laws will generate even more complex behavior in time.

Phillip E. Johnson (Wikipedia), considered one of the founders of the “Intelligent Design” movement (Wikipedia), and author of “The Wedge of Truth” (NCSE), claims, on page 54 of this book: 

“The heart of the problem is that physical laws are simple and general and by their nature produce the same thing over and over again.  Law-governed processes can produce simple repetitive patterns, as in crystals, but they cannot produce the complex specified sequences by which the nucleotides of DNA code for proteins any more than they can produce the sequence of letters on a page of the Bible.”

This book was published in the year 2000.  Yet it describes a simplistic understanding of physical laws at a level understood in the 1800s, when the mathematical and computational tools available limited our analyses to only the simplest of systems.  Mr. Johnson's comprehension of science would fail when confronted with the questions of radiation and the structure of matter that would emerge in the 1900s.

Many of 'problems' in physics that emerged at the close of the 1800s would require scientists to give up their simple ideas of how physical laws determine a system's behavior with time.  This expanded view of science would also revolutionize our technology, which in turn would change our society, yet another system that would change over time, i.e. evolve.

From Physics and Physicists: Rejection and Ridicule

A recent post over at the Physics and Physicists blog is certainly relevant to this blog.  All those who want to claim that mainstream science is resistant to new ideas should read Rejection and Ridicule.

Testing Science at the Leading Edge... II

Here's my next entry on science at the leading edge (see
“Real” Science vs. “Cosmological” and “Origins” Science, Testing Science at the leading Edge).  Here I present an example of how we do science when direct experimental verification is not possible, which I have labeled 'option 2' in the previous articles.

So what do we do if a particular experimental confirmation may forever be out of range for Earth-based laboratories, where current technology is not sufficiently sensitive to detect an effect, or too many resources are required to run it. 

If a theory predicts an effect is too small for current technology to detect directly, is that proof that the effect does not exist?

According to many pseudo-scientists, the answer to this question is 'yes'.  They use these 'gaps' in current understanding to squeeze in their outlandish claims.  To isolate the full implications from their belief systems, they have established the categories of “Origins Science” (for Young-Earth Creationists) or “Cosmological Science” (for Electric Universe supporters). 

But consider how foolish such a claim looks in the light of some historical examples.

In 1990, there were NO planets known beyond those in our own Solar System.  Was this proof that no extra-solar planets existed?  At that time, even our own Solar System would be undetectable by the technology of the day even if it were around the nearest stars.   While I've yet to find any documentation that any creationists advocated that our Solar System was unique in all the universe, such a position would certainly be consistent with many characteristics of their beliefs.

By the late 1990s, when the technology finally reached the point where some of the more extreme types of solar systems could be detected, some creationists went so far as to try to dismiss the detections (see Another Failed Creationist Prediction?).

But you might think that these types of problems can only happen when researchers must rely on observation alone.  It can't possibly happen in laboratory science where one has controls on the experiment.  Could it?

Consider another example from the laboratory...

In 1930, subatomic physics was in a turmoil because the process of beta decay seemed to violate conservation of energy, conservation of momentum, and even conservation of angular momentum.  Physicist Wolfgang Pauli postulated that an undetected particle, of very small mass, which did not respond to the electromagnetic or known nuclear force, could explain the discrepancy.  It would be called the neutrino.  With such an assumption, it became possible to construct a mathematical theory of how this particle did interact with other matter in the process of beta-decay and other interactions.  This theory enabled researchers to indirectly determine the characteristics of the particle, as well as refine the theory.  This work also enabled researchers to estimate the type of technology it would take to detect a neutrino in a more direct fashion.  This work would eventually pay off in 1955.

Lest these examples make one think that this case is only relevant in the more esoteric corners of science, and has no impact on our lives, consider the example from the previous part of Newtonian gravitation.

When humans launched the first satellites into orbit in 1957, there was NO laboratory confirmation of the inverse-square distance law of Newtonian gravitation!

Beyond the science fiction of Newton's day, did anyone seriously think that Newtonian gravity would or even could ever be subjected to a laboratory test? 

And if you relied on the astronomical observations, you just had two data points near the Earth - one on the surface, where the acceleration of gravity was measured as a constant to within the precision of the instruments, and the next one at the orbit of the Moon!  There were a few ballistic launches that covered some of this region, but the for most part, the theory of gravitation had 'gaps' that were hundreds of thousands and even millions of miles wide.

Yet with no laboratory confirmation, nations spent millions of dollars in a pursuit to launch satellites into orbit.  This was an effort that actually took a number of years to accomplish.  None of the nations involved started from zero - both Russia and the United States were actively pursuing these goals, but it was not until the launch of Sputnik was it clear that who was ahead in the effort. 

If the residents of a nation believed that only laboratory confirmation of a theory was sufficient to regard a theory as valid science, would they be willing to spend millions of dollars developing the capability to orbit satellites?  

What would the world be like today if U.S. science had adopted such a 'laboratory-only' policy on what qualified as science?

There are a few other examples I've found in scientific history where development of a critical technology would hinge on the reliability of astronomical observations.  I'll save some of those for a future article.

Electric Universe: Do I Have Any Readers in the UK?

Actually, it is a bit of a rhetorical question as Google Analytics and e-mails indicate that I do have some readers in the UK and some are professional astronomers.

There is apparently an upcoming talk by one of the 'High Priests' of the Electric Universe (EU), taking place in Surrey, UK (just south of London) on Saturday, July 10, 2010.

Wallace Thornhill: 'Exploring the Electric Universe' (link to details)

The web site suggests questions be submitted in advance, with a deadline of May 31 (drat!) but only for those who will be in attendance.  However, it  appears the floor may be open to questions.  Perhaps some professional astronomers may attend who are sufficiently familiar with the EU problems that they can ask some insightful questions.

Note that I am NOT advocating any kind of confrontation with the speakers.   The nature of British libel law makes this particularly hazardous (See LibelReform.org, SenseAboutScience).  Indeed, due to the nature of British libel laws, it might be far more useful to listen carefully to how EU talks about their critics.

Most of these types of presentations I've attended by creationists and others, I have kept quiet, though I would often participate in conversations among the audience before and after the presentations.  Even professionals should be very wary of confrontations in these environments.  When it comes to questions, I have often, but not always, seen a limiting technique similar to that mentioned above, where the questions must be presented in advance.  That way, the audience need never know which questions the presenters actually try to evade.  When I have asked questions of the speaker, I have tried to keep the focus on my specific question rather than allowing the speaker to divert the question into other topics.

Here's my questions which I have sent to the site.  Since I will not be in attendance, Mr. Thornhill may feel free to ignore them, but I suspect there will be some in his audience who will be very interested in the answers,  Since I've made them available here a month prior to the talk, allowing Thornhill plenty of time to prepare a real answer, many in his audience will know if he ignores them.

1) Hannes Alfven received his Nobel prize (Nobelprize.org) for the accomplishment of making certain types of plasmas mathematically tractable.  Langmuir (1913PhRv....2..450L, 1924PhRv...24...49L) and others were developing other mathematical models of discharge plasmas predating Alfven.  REAL plasma physicists continue to revise the mathematical models and these models have improved significantly.  Even the classic discharge graphic in Cobine's “Gaseous Conductors” (pg 213, figure 8.4) has been modeled with Particle-In-Cell (PIC) plasma modeling software (see Studies of Electrical Plasma Discharges, figure 10.1).  Plasma models, some sold as commercial software, are also used to understand the plasma environment in a number of research, space, and industrial environments (see VORPAL).  Why do Electric Universe supporters consistently dismiss the use of mathematical modeling of plasmas?

2) Astronomers have studied about the effects of free charges and electric fields in space as far back as 1922 (1922BAN.....1..107P) and 1924 (1924MNRAS..84..720R).  Note that this work predates Langmuir coining the term 'plasma' for an ionized gas (1928, 1928PNAS...14..627L).  Rosseland and Pannekoek's work is still cited today since gravitational stratification is one of the easiest ways to generate and sustain an electric field in space.  Why do EU supporters continue to claim that astronomers ignore electric fields and free charges in space?

3) Space weather forecasting is vital to protecting the lives of  astronauts as well as billions of dollars in satellite assets.    The different professional computational models used by NASA, NOAA, the U.S. Air Force, U.S. Navy, etc. (CCMC) agree very well on large-scale behavior of coronal mass ejections and other space weather events.
a) Where is the Electric Sun model that can compute the particle fluxes, energies and fields from first principles which are consistent with the measured solar luminosity and in situ spacecraft particle and field measurements?
b) If EU does not publish its models where they can tested against other models as well as measurements, how can they claim they are doing science? 

4) Mainstream solar physics uses Doppler imaging of the solar surface to construct images of the farside of the Sun (see Acoustic Imaging of the Entire Farside of the Sun).  Now the STEREO spacecraft are approaching positions where we will finally see almost the entire sphere of the Sun and will be able to conduct more direct tests of this capability (see STEREO: Comparison with GONG and MDI farside maps).  This capability critically depends on our understanding of the solar interior, yet EU claims that all our models of the solar interior are wrong.
a) If mainstream models of the solar interior are so wrong, why does this technique work at all?
b) All of the solar data for this capability are PUBLIC (see MDI Data Services & Information) and the software runs on desktop-class computers you can buy at almost any computer store.  So when will EU demonstrate that their Electric Sun model can generate equivalent or better results?

5) Every book on how to write applications & interpret the signals from GPS satellites emphasizes the importance of relativity in converting these signals into a high-precision receiver position (see Scott Rebuttal. I.  GPS & Relativity).   Yet EU supporters deny the importance of relativity in this application.  Has any EU supporter designed and built a working high-precision GPS receiver that can be certified as free of relativistic corrections?

6) Mainstream astronomy and astrophysics has guided science into pioneering discoveries in gravity, with the application of space flight, and atomic and nuclear physics, with the applications of semiconductors and materials science (see The Cosmos In Your Pocket).  Humans have moved into space without one single model that yields testable measurements from the Electric Universe supporters.  What does EU provide that is not already provided by mainstream astronomy and geophysics?

I could add a significant number of additional questions, many of which are also asked in my many blog posts on EU, but this is getting a little long already.

If anyone following this blog manages to attend this event, I would enjoy hearing about it.

Neutrino Oscillations: Yet Another Blow Against Non-nuclear Stellar Energy...

Attempts to further refine and characterize the nature of neutrino oscillations achieved another significant milestone recently with the report of the first neutrino event detected in the OPERA (Oscillation Project with Emulsion-tRacking Apparatus) experiment.  In this experiment, neutrinos generated over 700 kilometers away at CERN (see Particle Chameleon Caught in the act of Changing) would travel through the Earth to be detected by OPERA.

Various science press sites carried word of the announcement

• Wired: Elusive Neutrino Change-Up Finally Detected
• Physics World: Double celebration for neutrino lab
• PhysOrg.com 'Neutrino oscillation': Particle chameleon caught in the act of changing

The Solar Neutrino problem (Wikipedia) had been a long-standing problem in solar physics.  The initial recognition that the number of electron neutrinos detected at the Earth was only about one-third the number actually predicted from the Standard Solar model (Wikipedia) goes back to the late 1960s.  

Numerous alternative explanations for the neutrino deficit were explored, including ideas such as non-thermal distributions of particle energy (link), and even a black hole at the solar center (link).  Neutrino oscillations gained favor as these other hypotheses fell due to their inability to account for other measurements.  Neutrino oscillations had the advantage that they could be below the detection limit of Earth laboratories of the day and still explain the deficit.   But even that 'advantage' would yielded to improved experimental techniques precision.

Due to the many years it would take to find a solution, the solar neutrino problem has been exploited by creationists and other pseudo-scientists as evidence for their own particular non-nuclear theories of stellar energy generation.  This has includes some Young Earth Creationists (though more creationists are including the solar neutrino problem on their list of arguments creationists should NOT use), electric stars (check out 'Electric Sun' in the tag cloud of this blog) and others.

In 2001, the Sudbury Neutrino Observatory (SNO)(wikipedia), which is sensitive to all three flavors of neutrinos, would detect the 'missing' neutrinos (SNO First Scientific Results)

Such particle-type oscillations (FNAL, Wikipedia) are not unheard of in particle physics.  The first such case was discovered in the 1950s and was known as the Theta-Tau Puzzle.  Refined experiments eventually isolated the curious result to unusual properties of a single particle which is now called the Kaon (Wikipedia).

Responses from various pseudo-science supporters to this news has ranged from avoidance of the announcement, to denial, to accusations against the scientific community.  Not unexpected.  Such 'non-nuclear sun' advocates have yet to produce a neutrino flux estimate calculated from first principles (their claimed model of stellar structure combined with neutrino production physics) without the model having more severe problems with other measurements.

216th Meeting of the American Astronomical Society

I've been busy the past few weeks on family business, vacation travel, and the 216th meeting of the American Astronomical Society (AAS) meeting in Miami, FL.  As part of the vacation, we visited Key West and Kennedy Space Center.

For the AAS meeting, I converted some of my “Cosmos In Your Pocket” material into a poster which generated a fair amount of interest and suggestions for expanding and publicizing the effort. 

I participated in a number of informal discussions on pseudo-science issues with several attendees with whom I hope to develop some useful collaborations.  A growing number of science professors working in classroom environments have begun integrating lessons dealing with pseudoscience issues into their regular courses.  In discussions with some scientists at major scientific facilities, just the mention that I explored crank science issues elicited numerous stories of encounters with advocates of some astronomy-related crank science.

There was a poster presentation by some individuals from Bob Jones University with Danny Faulkner (University of South Carolina, Lancaster) as one of the co-authors.  Dr. Faulkner is a Young-Earth Creationist who is a graduate of Bob Jones University.  In spite of several visits to this poster, I did not get a chance to speak to the authors(s).  A copy of the content was available and I took one for further examination.  The poster was a description of observations of an eclipsing binary star, FY Bootis.  The poster appeared to be an analysis of the orbital elements of the binary system using the standard tools used by astronomers, and I could find no insinuations or implications of any significantly different cosmological interpretations.

I saw no posters by individuals identifiable as supporters of Electric Universe claims.  However, there were numerous posters on studies on plasmas in space and the laboratory so the popular EU claim that astronomers ignore effects of electromagnetism in space just keeps sounding more and more hollow.

• Formation and Reconnection of Three-Dimensional Current Sheets in the Solar Corona
• Instabilities of Current Carrying Torus
• Reconnection Outflows and Current Sheet Observed with Hinode/XRT in the April 9 2008 "Cartwheel CME" Flare
• Electron Beam Return-Current Losses in Solar Flares: Initial Comparison of Analytical and Numerical Results

I attended a public talk, sponsored by the AAS & AIP, of the Gemant Award (Puerto Rican-Uruguayan astronomer Daniel Altschuler wins AIP's 2010 Gemant Award).  The title was “Science, Pseudoscience and Education”, presented by Dr. Daniel Altschuler (NAIC-Arecibo Observatory).   Dr. Altschuler advocated, as I have, using pseudoscience as a teaching tool.

I sat in on Gerrit Verschuur's (University of Memphis) presentation of correlations between high-velocity HI clouds and WMAP 'blobs' (On the Association between WMAP and Galactic Neutral Hydrogen Small-scale Structure).  The basic thesis appears to be that some WMAP bright points, or “hot spots”, appear correlated with regions which may be collisions between high-velocity HI clouds.  The collision ionizes some of the hydrogen and the free electrons create emission in the bands where WMAP can detect it.  Some groups supporting alternative cosmologies (including some which are clearly pseudo-science) have tried to use Dr. Verschuur's work as evidence against the Big Bang.  From the presentation, it was unclear if the exclusion of these hot spots (if indeed they are created by cloud collisions) would sufficiently alter the WMAP power spectrum to create problems for the Big Bang cosmological model.