Among scientists, the term “Evolution” by itself is usually assumed to mean biological evolution. There are a number of other scientific uses of the term that are usually referenced with a qualifier. In astronomy, there are subfields such as stellar evolution and cosmic chemical evolution and similar uses of the term 'evolution'. All of these terms refer to how the structure, chemical abundances, and other characteristics of astronomical objects changes with time.
When wielded by a creationist, the term 'evolution' can mean any or all of the above. In arguments, they will often lump Big Bang cosmology in with their claims about biological evolution.
But in this case and others, it reveals yet another fundamental misunderstanding among creationists:
Evolution is built into the very fundamental physical laws that govern the Universe.
Evolution in time is a part of every major physical theory. These theories incorporate the behavior of some measurable property as time progresses. This characteristic is incorporated into the mathematical form of the theory through a term called a time derivative (Wikipedia). There are two popular forms used to designate time derivatives. There is the total derivative (Wikipedia) of, for example the quantity, f, with respect to time,
and the partial derivative (Wikipedia), with the more unusual symbols
(The details how these two forms are used in physics and mathematics are not really relevant to this discussion.)
The derivative most people would be familiar with is the speedometer on their car. Speed is the time derivative of distance traveled (so the speedometer displays the time derivative of the odometer). Conversely, the odometer in the integral of the speedometer, adding up the different speeds at different times to compute the total distance traveled.
Here's some of the fundamental theories where change with respect to time is an important part of the theory.
- Newton's theory of motion and gravitation
where the force, F, is defined as the change in momentum with time, and this is equated to the gravitational force. Note that in the case of gravity, the force is directed along the line between the two masses, designated M and m. The full 3-dimensional form of this theory is used for predicting where planets and asteroids move with time, as well as the engineering application of moving human-made satellites around in space.
- Maxwell's electromagnetism
Here, the equations are much more complex than Newton's theory of gravity. This complexity is related to the coupled nature of electricity and magnetism. The quantities in bold represent 3-dimension vector fields, in this case, the electric field, E, and the magnetic field, B. The inverted triangle symbol, called nabla, is called an operator, which does specific manipulations on vector quantities. In general, E and B can vary in space as well as time. In this equation, the time derivative is a partial time derivative. These equations are applied in the design of electrical circuits, especially circuits which use custom-designed components, as well as antenna design and the study of plasmas.
- Schrodingers equation
This equation solved the mysteries of atomic structure and chemistry. While the equation might look trivial, the quantity H is not a variable but an operator, similar to the vector operators above, which is a mathematical form the contains information about how energy (kinetic and potential) are stored in the system. This equation not only solved the mystery of atomic spectra (Wikipedia) but also the structure of matter and provided the foundations of semiconductor electronics. Today this equation is solved on computers for complex molecules to determine their properties before they are synthesized in the lab, the field of Computational Chemistry (Wikipedia).
I could describe more, but these three fundamental equations actually form the basis of much of the technology we've have developed in the twentieth century and how the system changes with time is part of every one of them!
Solving any of these equations for a general system, with time dependence, is a very difficult task. It is only in the past fifty years or so, with the advent of modern computers, that progress has been made in realistic systems. Prior to modern computers, the analysis was often restricted to systems with simple behavior in time, or even static, steady-state systems, where the time derivative is actually zero. In this case, solutions could often be found through combination of known mathematical functions. Mathematical techniques did not exist to solve them in the more general applications, or they had to be solved numerically by hand and were so tedious and complex it might take a researcher years just to solve a small system, assuming they didn't make a mistake.
Much of engineering is based on steady-state, or static solutions. Many of the textbook formulas that engineering students are often taught to accept as 'gospel' are often derived by physics students from more fundamental physics principles. You want a bridge to be a stable structure for a long period of time so you look for solutions to the equations where the time-derivative of the velocity is zero - where all the forces exactly balance - indicating that it is a fixed solution for the system. Most people prefer these characteristics in the products they purchase, from their homes to their cars. They want any change in the system with time to be slow, to make the life expectancy of their purchase long.
But around 1900, researchers were beginning to realize that the simple, steady-state systems that they were studying mathematically were just the tip of the iceberg when it came to what was possible with these so-called 'simple' mathematical principles behind physics. Even relatively simple physical principles, expressed as differential equations (Wikipedia) could yield surprising complex solutions that were not regular, and had many characteristics that, at first glance, might be regarded as random.
This new complexity arises as we try to analyze more complex systems and the physical laws must be 'coupled' in different ways, making the resulting equations a nonlinear system (Wikipedia). For example, the Lorenz attractor arises in the study of convection, where where the density of a gas at different temperatures becomes a driving force under the action of gravity (Wikipedia).
Consider the case of stellar evolution. Astrophysicists first studied simple stars in a steady-state configuration. They were able to do this using just the theory of gravity and the gas laws, before it was known that stars were powered by nuclear reactions. Later, they realized that the nuclear reactions in the core of the star would change the composition of the core and this composition change would change the behavior of this hot plasma which would change the structure of the star. In turn, the change in structure would create changes in the nuclear reactions and this feedback mechanism would create a situation where the star's structure and composition would change over time. That is stellar evolution in a nutshell, a picture that did not reach observational, experimental, and theoretical maturity until the latter half of the 20th century.
As we analyze more complex systems, it becomes clear that these couplings between different physical laws will generate even more complex behavior in time.
Phillip E. Johnson (Wikipedia), considered one of the founders of the “Intelligent Design” movement (Wikipedia), and author of “The Wedge of Truth” (NCSE), claims, on page 54 of this book:
“The heart of the problem is that physical laws are simple and general and by their nature produce the same thing over and over again. Law-governed processes can produce simple repetitive patterns, as in crystals, but they cannot produce the complex specified sequences by which the nucleotides of DNA code for proteins any more than they can produce the sequence of letters on a page of the Bible.”This book was published in the year 2000. Yet it describes a simplistic understanding of physical laws at a level understood in the 1800s, when the mathematical and computational tools available limited our analyses to only the simplest of systems. Mr. Johnson's comprehension of science would fail when confronted with the questions of radiation and the structure of matter that would emerge in the 1900s.
Many of 'problems' in physics that emerged at the close of the 1800s would require scientists to give up their simple ideas of how physical laws determine a system's behavior with time. This expanded view of science would also revolutionize our technology, which in turn would change our society, yet another system that would change over time, i.e. evolve.
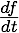




4 comments:
I just wanted to note that on the right-hand side of Schrödinger's equation there is no derivative with respect to time. ;)
Apart from this a very nice article, as usual! Keep up the good work!
Thanks. It's been corrected.
The gravitation equation has a missing two in the denominator.
Fixed. Thanks.
Post a Comment